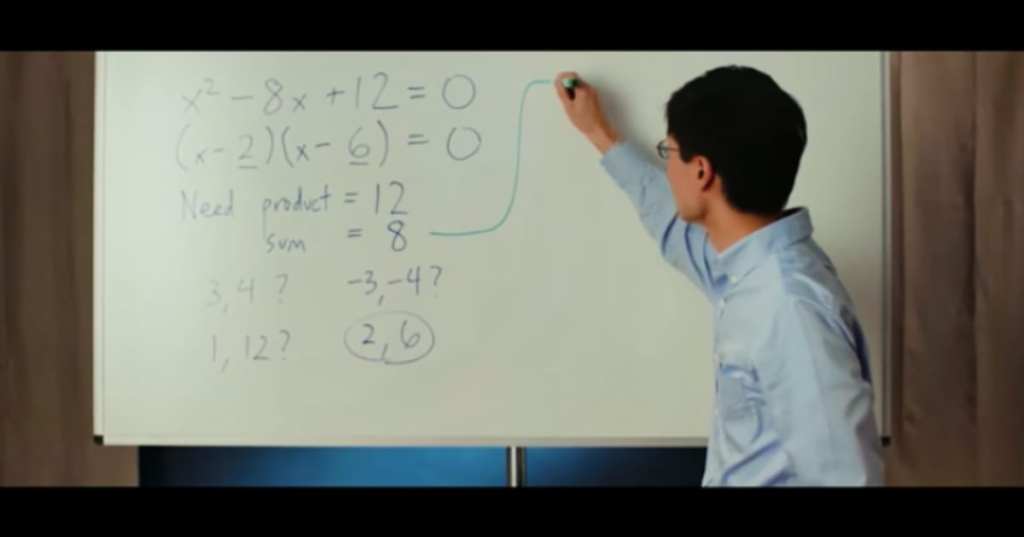Ok, ok, fine – he never said it was easy, just that it was easier, but I mean…are we buying that? I’m not someone who thinks any sort of math(s) are easy, not even the kind that sixth graders are assigned for homework, so I remain skeptical.
Still, let’s give Dr. Po-Shen Loh of Carnegie Mellon University a chance to explain himself, shall we?

Image Credit: YouTube
Quadratic equations are polynomials that include an x². Teachers use them to have students learn to seek two solutions at once, which typically involve methods like completing the square – but Dr. Loh turns finding roots into a few simpler, intuitive steps.
Polynomials are strings of math terms that can have one or many variables, and depending on how many times a line crosses any particular latitude or longitude, can have a solution with one value or two root values.

Image Credit: YouTube
Dr. Loh uses the idea of the two roots of every quadratic equation to make a simpler way to get to those roots by describing them this way: combined, they average out to a certain value, then there’s a value z that shows any additional unknown value. Instead of searching for two separate, different values, we’re searching for two identical values to begin with. This simplifies the arithmetic part fo multiplying the formula out.
He believes this is a more intuitive way for students to learn, since there’s no special or separate formula required – all students need to do is remember some simple generalizations about roots, and they can decide where to go next.
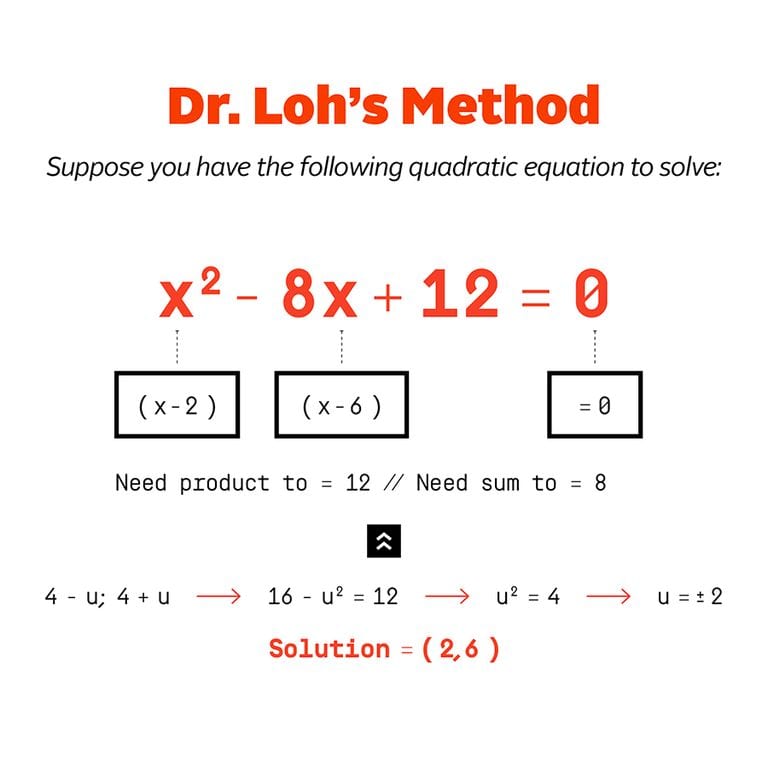
Image Credit: Dr. Loh
Since understanding quadratic equations is a key to grasping precalculus (and maths beyond), this could really help kids who are struggling.
If you ask Dr. Loh, what he’s tried to do is to build a bridge between understanding how concepts work in a classroom setting and ways to apply the ideas in the real world, and that’s pretty fun no matter who you are.
Here’s a video that explains the method in depth.
I’m still not sure that work as a mathematician is in my future, but I can understand enough of this to realize what a cool thing he’s done for students all over the world.
If you are a math person, tell us what you think of this development down in the comments!