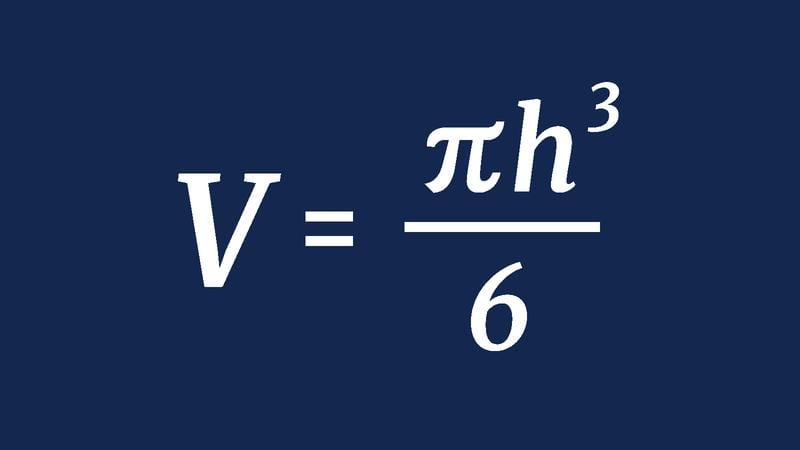Let’s begin with this mind-blower: If you cored an orange, and cored the earth, and the remaining rings were the same height, they would have very different diameters, but the same volume.
Say what?
https://www.instagram.com/p/BwX6ze0g8Te/
It’s true. The so-called “napkin ring problem” dates back to the 17th century and Japanese mathematician Seki Kowa, who dubbed the shape left over when you core a sphere an “arc ring.”
Or, a “napkin ring,” since it kind of looks like a classic napkin ring.
Here’s what it means:
When you core a sphere, you must remove a cylinder-shaped section from the middle, leaving a ring behind. No matter what size of sphere you start with, every arc ring (or napkin ring) with the same height will also have the same internal volume – no matter its diameter.
Here’s the non-math explanation: As the size of the sphere grows, so does the size of the cylinder you’re going to remove. The smaller the sphere, the thicker the napkin ring, and vice versa.
In order to formulate the volume of each napkin ring, you have to first formulate some equations that use the area of a circle, use some geometry, and put your Pythagorean theorem into use – all of which leaves you with this: